Mathematica 13破解版 v13.0 中文版

Mathematica 13是一款专业性极强的计算系统软件，相信从事数学教育行业的用户一定经常需要进行计算。所以小编在这里为你带来了Mathematica 13汉化版，在老版本的基础上将数值、编程语言、文本与其他应用功能于一体，满足不同用户的使用需求，大大提高了工作效率。

Mathematica 13最新版界面简约清爽，功能一目了然，而且支持简体中文，从此再也不用担心语言问题。最重要的是，操作十分简单，不需要投入太多的时间学习，即使是新手也能快速上手使用，需要的小伙伴快来下载体验吧！

Mathematica 13安装破解教程

1、从本站下载解压后，即可得到Mathematica 13源程序和破解文件

2、双击“Setup.exe”文件运行，默认中文简体语言，开始安装

3、选择软件安装路径，一般默认即可

4、选择安装组件，建议默认安装即可

5、耐心等待软件安装完毕（时间稍长），完成后可直接启动程序，选择【Finish】按钮即可退出向导

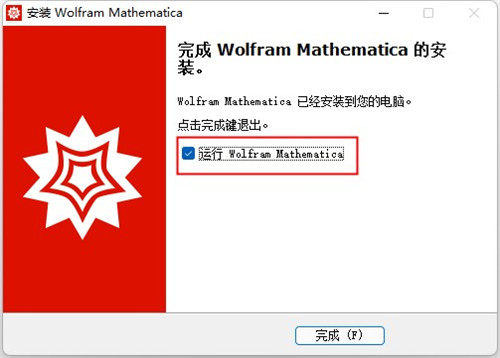
6、首次启动Mathematica 13，软件自动弹出注册提示，选择“其它方式激活”如下图所示：

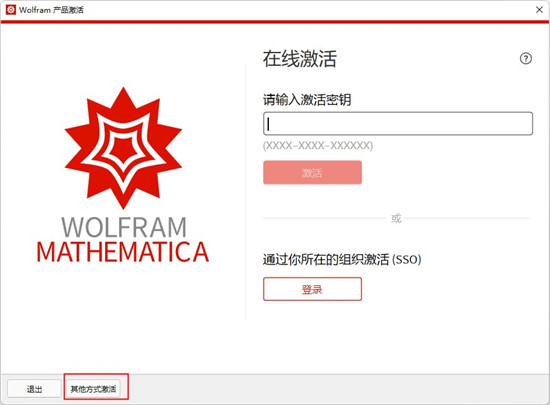
7、选择“手动激活”

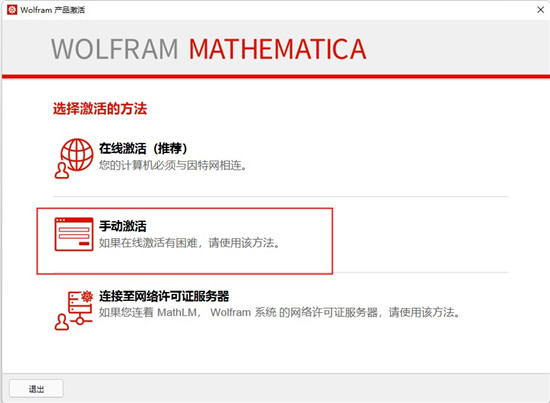
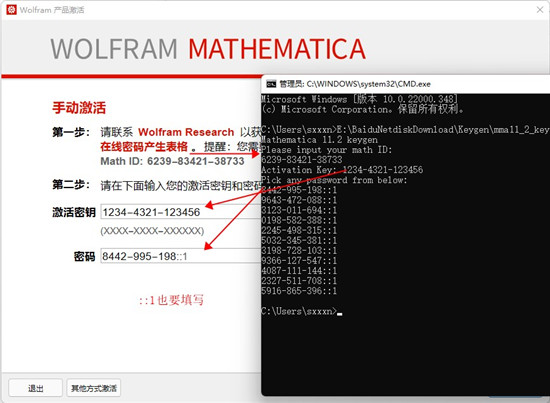
8、打开CMD（以管理员身份）并输入：cd C：\

然后输入mma11_2_keygen_64.exe（我会像这样：C：\ mma11_2_keygen_64.exe）再在CMD中键入您的MathID并生成许可证

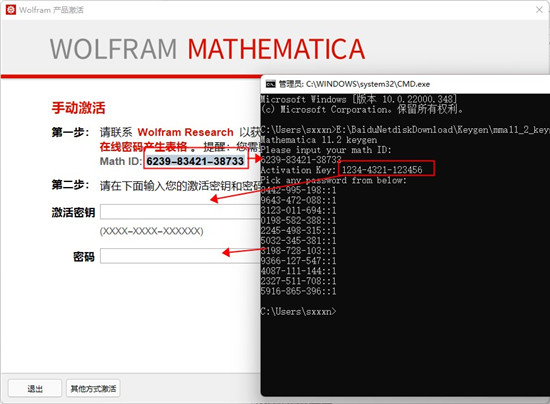
9、将破解补丁的激活密钥和密码复制，注意::1这个也要复制

10、同意条款点击下一步。

11、至此，软件Mathematica 13中文破解版已破解完毕，所有功能可随心免费使用。

mathematica怎么运行

Mathematica这个软件有时候很耗时。

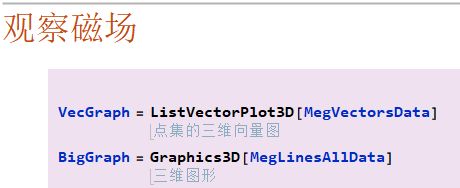
常见情形1：绘图计算特别耗时。比如这段绘图数据计算用时60min.

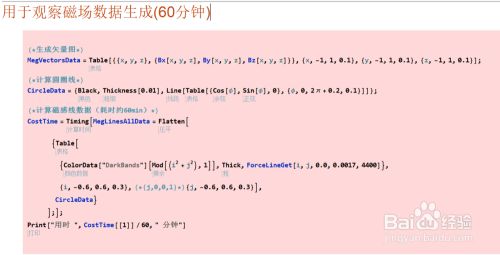
然而将算好的数据呈现出来却只需要几秒钟。

（Tips: 通常先计算Table数据，然后就可以使用ListVectorPlot替换VectorPlot, ListStreamPlot替换StreamPlot 等等, Graphics3D这些只负责根据数据画图的函数，可以将 运算数据 和 调整绘图样式 分开。）

常见情形2：数值求解微分方程特别耗时。比如这个耗时18分钟。

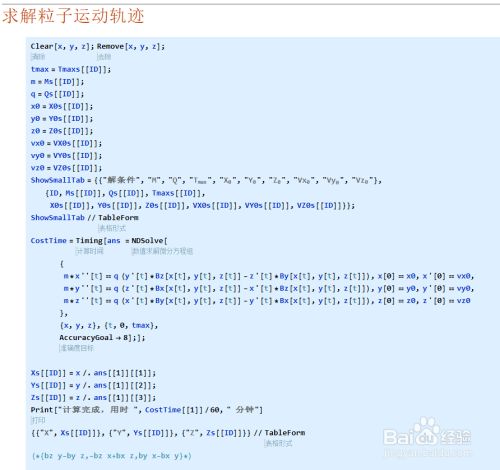
以上这两种情况有一个共同点，就是我们没法简单的把计算结果导出成字符串存在记事本里。并不是1+1=2，把2复制下来那么简单。

第一种情况的绘图数据里面有颜色/样式等无法表达成字符串的数据类型，第二种情况，运行结果是几个插值函数。

还有其他情况等等。很多时候我们很长时间算出来的东西也许是个插值函数，也许是一个动画，也许是一个复杂的图形，也许是一个数据类型庞杂的列表。

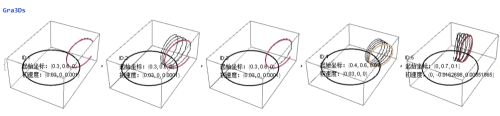
序列化既然不能保存这些数据，那么就应该二进制存储。还好Mathematica提供一种二进制数据交换格式WDX, 可以将内核中的形态各异的数据原封不动的存到文件里。

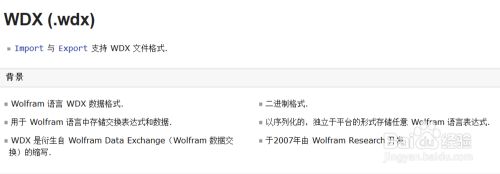
Export导出WDX的基本用法:

Export["文件路径/文件名.wdx",待存储符号,"WDX"]

Import导入WDX的基本用法:

待读取符号=Import["文件路径/文件名.wdx","WDX"];

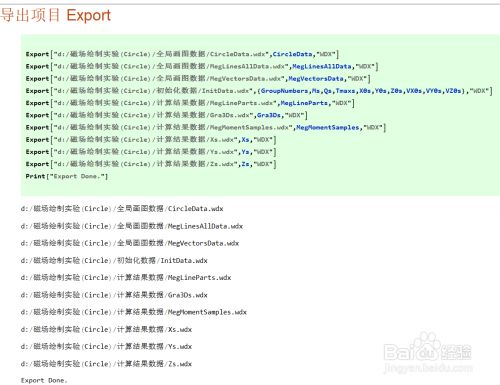
WDX可以接受任何变量，也许是一个Plot图像，也许是一个列表，也许是一个函数。当然，运算结果可能有上百MB.

mathematica使用教程

一、【基础运算操作】

1、运算符：Mathematica支持我们常见的运算符+ - * / ^ ! （加，减，乘，除，指数，阶乘）。逻辑运算符&&与，||或，！非

2、表达式：在Mathematica中可以直接将字母符号带入运算，这在大部分的数学软件中是不允许的，如x+y+y=x+2y（字母符号的运算）f=2x（定义一个含有字母的表达式）。

3、书写操作：主要有两点①回车表示换行，Shift键与回车同时按下表示执行程序。②一个表达式以分号；结尾则不输出结算结果，一行可以写多个表达式，但是需要用分号分隔。

4、百分号的用处：%表示上一次的计算结果。

5、内建函数：Mathematica有很多强悍的内建函数，通常以大写字母开头，如常见的Sin[]正弦函数，Plot[]用于函数绘制，Expand[]用于多项式展开等。（注意Mathematica是区分大小写的，所以在写函数时一定注意开头大写，另外紧跟中括号，不要写成小括号。认识并使用常见的内建函数是用好Mathematic的重要途径，在后面会有更加详细的介绍）

第一节基本知识的举例如下：

二、【常量和变量】

1、常量：在Mathematica中常量有整数，有理数，实数，复数和内置常数，特别要说的在附属中，虚数单位用I（大写的i）表示。内置的常数有Pi（圆周率），E（自然对数），Infinity（无限大）等组成。

①、常数的转换：这里常数的转换指的是将数字转化为有理数或者实数，这里就要用到两个内建函数啦（还记得内建函数的知识吗？见1.5）N[x,n]可以将x转化为实数，精度位数为n其中n可以省略，Rationalize[x,dx]将x转化为有理数，误差小于dx

②、数的输出：NumberForm[x,n]将x以n位精度的实数输出，ScientificForm[x]将x以科学计数法的形式输出

2、变量：变量名是字母和数字的组合，其中不能以数字开头，a12是合法的变量名，12a是不合法的变量名（在说变量名能不能用的时候，通常会用“合法”，“不合法”来表示，合法即这个名称可以作为变量名，反之则不行）。在有乘法存在的时候有些人会把乘法和函数名弄错，如x=2;y=3;之后很多人会将xy理解成乘积，实际x*y才是乘积，xy只是一个新的你没赋值过的变量。

①、变量的赋值：变量赋值用等号=来实现，绝大多数编程语言都是，批量赋值可以用大括号加等号{x,y}={1,2}这样x,y就分别等于1或者2了。当你不使用变量是可以给变量一个空值用x=.来实现

②、变量的替换：使用/.和->箭头可以用来替换表达式中变量的数值（还记得什么是表达式么？看看1.2）执行（还记得怎么执行一个语句吗？看看1.3①）f=2x只可以得到f=2x，再执行f/.x->2就可以得到4，也就是将式子中的x用2替换。多变量的时候用f/.{x->1,y->2}来用值替换变量。

③、变量的删除：Clear[]可以用于删除一个变量，在Mathematic里面变量一旦定义就固定了，所以如果多次使用f这个字母可能出现问题，那么我们要定义新的f的时候就需要用Clear[f]将其删除后再重新定义，这点很重要，尤其是在程序变量很多的时候

三、【函数，表和逻辑表达式】

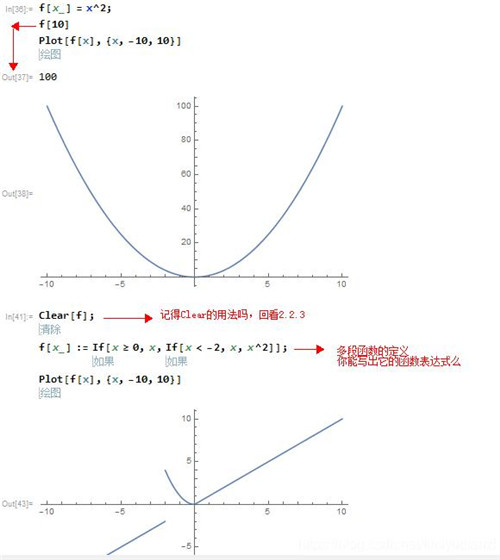
1、函数分为自定义函数和内建函数，这里再列举几个常见的内建函数，如Log[]，Round[]四舍五入，Max[]取最大值，Exp[]指数函数，Cos[]余弦。自定义函数的用法是f[x_]=表达式，如表达式可以是x^2，这里的自变量用x_表示，如果是多变量的函数就用f[x_,y_,z_]来表示。除了用等号来定义以外还可以用f[x_]:=表达式，即冒号加等号来定义函数叫做延迟定义，延迟定义的意思是你现在写的只是一个式子，程序并不执行，等到你第一次调用该函数的时候系统才会真正定义（如果你看不懂延迟定义的话不要紧因为不重要，你只要知道冒号等号：=的含义和等号=都是可以定义函数的就可以了）。

①、分段函数的定义：分段函数定义需要使用内建函数If[]，如x大于等于0时函数值等于x，函数值小于x时等于x^2，那么我们就应该这样书写该函数f[x_]=If[x>=0,x=x,x=x ^2]。也可以用If实现多段函数的定义。

②、函数调用，调用函数时，不需要像2.2.2那样用替换实现，只需要用f[1]就可以给自变量x赋值了

③、函数的显示：为了直观的展示函数的样子我们用Plot[]绘图功能对函数的样子进行展示，首先我们要定义一个函数或者是一个表达式，用法是Plot[f[x],{x,min,max}]即展示函数f，自变量为x，x的最小值为min最大值为max。（Plot还有很多高级的用法，比如为坐标轴加标注等等，可以绘制出很多漂亮的图形以及三维的图形，这里不详细描述，有需要可以寻找其他资料详细了解）。

2、表：将一些相互关联的元素放在一起就是表，这并不是一个新的概念，2.2.1函数的赋值中{x,y}这样的用法就是一个表，或者叫一个向量，也可以将表达式写成一个表{x,x2,x3}针对表也有很多的操作，这里有个概念就可以了。

3、逻辑表达式：除了数字之外，还有一部分变量用来刻画逻辑，如判断两个变量是否相等的时候用 == 两个等号进行判别，注意不要和赋值运算混淆。常见的有x==y如果x和y相等则返回True，如果不相等则返回False，还有x!=y不等于，x>y大于，x>=y大于等于等等

四、【方程】

前面说了很多Mathematica的基础用法，有人会说这些用法大部分的编程语言都能见到，那么接下来我们就通过方程来展示下Mathematica的优越。

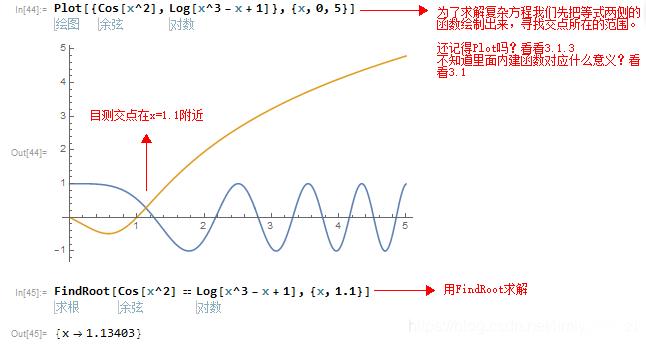
1、方程的表示：以上我们讲到了= 赋值和 = = 判断相等这两个符号（看看3.3）因为等号是赋值的，而我们通常将方程看为一个恒等式，其意义和赋值有一定的区别，所以我们这里用 == 来表示方程的恒等关系，如定义方程：x^2+2x+1==0

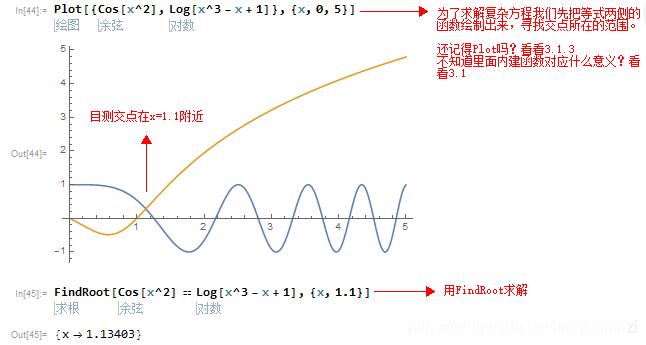
2、方程的求解：解方程需要用到Mathematica的几个内建函数，Slove[等式,{x}],Roots[等式,{x}],FindRoot[等式,{x,x0}]，Mathematica总能对不高于4次的函数精确求解，其中Solve和Root用法相同，FindRoot针对解十分困难的方程时，我们通过图像大致知道解的范围，那么我们指定x0，程序会寻找在x0附近的一个解。

3、解方程组，我们也可以用Solve解方程组的根，如Solve[{x+y= =0,x+2y= =6},{x,y}]

4、求方程组的通解，在有变量表达式的方程求解时，Solve[]只能给出部分的解，为了得到各种情况的解我们用Reduce[]来实现，这段话可能说的比较模糊，我们看下面的例子：

五、【微积分的常见操作】

.1、求极限：极限Limit[表达式,x->x0]表示当x趋近于x0时表达式的极限，如何求x趋近于无限大时的极限呢？看看2.1。

2、求微分：微分使用内建函数D[]实现，求f关于x的微分用D[f,x]表示，求f关于x的n阶微分用D[f,{x,n}]表示，求f关于x1，x2的双重偏微分用D[f,x1,x2]表示（D[]的功能非常强大，你可以尝试用此实现链式法则求导）当f函数为单变量的时候求微分也就变成了求导数，用Dt[]函数，其效果和D[]一致

3、求积分：积分使用函数Integerate[]实现，用法为Integrate[f,x]或者Integrate[f,{x,min,max}]前者计算函数f的不定积分，后者给出积分的上下限，计算函数的定积分。注意不是所有的函数都可以计算出不定积分或者定积分，也正因如此引出了数值积分的概念，数值积分使用指令NIntegrate[f,{x,min,max}]用数值计算的方法求得积分的近似值（这里开头的两个字母NI都是大写）。如果说积分函数在给出的下限和上限之间有不连续的点，那么我们需要将点补全

六、【微分方程的求解】

1、微分方程求解：微分方程的求解使用Dsolve[]来完成，其中导数使用跑撇号’表示，n阶导数用n个’表示，如求解y关于x的微分方程DSolve[{微分方程},y[x],x]。求解微分方程组的时候使用DSolve[{微分方程1，微分方程2},{y[x],z[x]},x]，求解带有初始条件的微分方程组DSolve[{微分方程，初始条件1，初始条件2},y[x],x]。

2、微分方程的数值解：与积分一样有的微分方程没法给出准确解，所以使用数值方法逼近，NDSolvep[{微分方程，初始条件},y,{x,min,max}]用这个方法可以求得微分方程的数值解，方法类似。

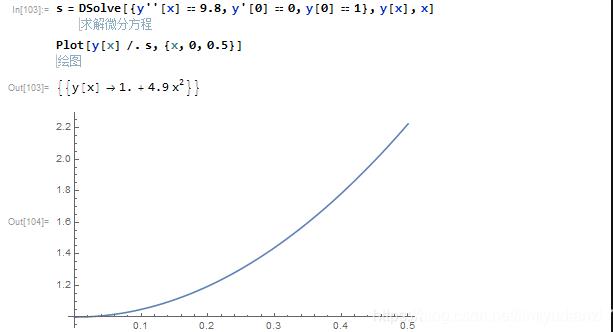
3、微分方程结果的展示：为了绘制微分方程我们需要用一个变量不如s表示问分方程的解，如：x关于y的微分方程s=DSolve[… …]，之后使用Plot[y[x]/.s,{x,min,max}]

mathematica怎么画图

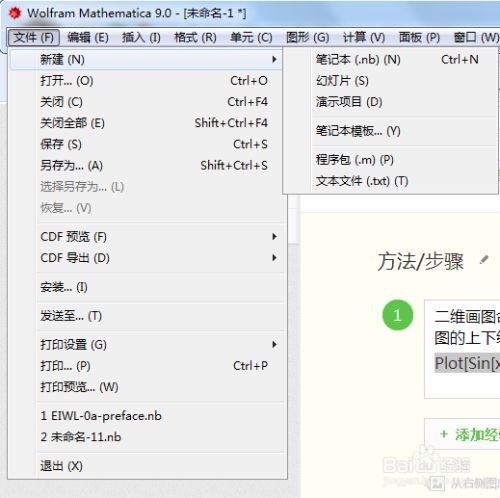
首先打开mathematica，然后文件--》  新建--》笔记本， 这样就完成了画图的基本工作。

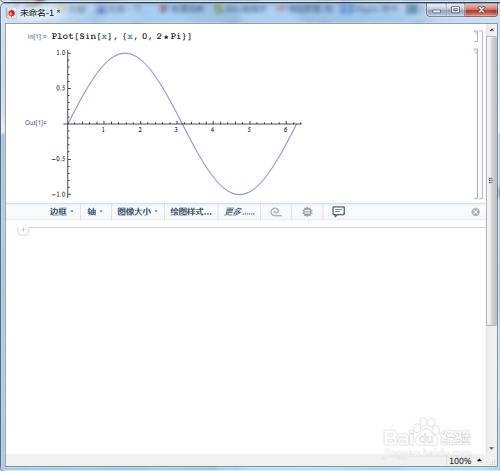
二维画图命令：Plot[f(x), {x,a, b}]   这里f(x)代表你要画的函数，a ，b代表所画图的上下线

Plot[Sin[x], {x,0, 2*Pi}]

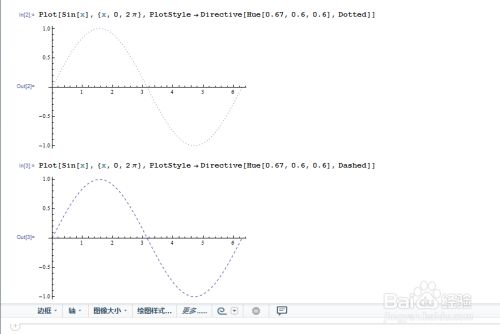
如果需要画虚线或者点线，可以用如下命令：

Plot[Sin[x], {x, 0, 2 \[Pi]}, PlotStyle -> Directive[Hue[0.67, 0.6, 0.6], Dotted]]

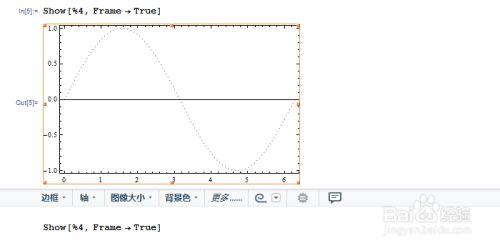
如果需要加入边框，输入： Show[%4, Frame -> True]； 这里%4  代表所画的第几个图片

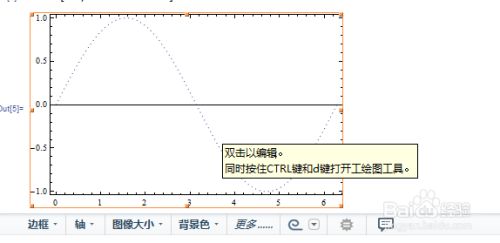
另外对于所画曲线的形式，以及边框的添加，曲线的颜色，背景颜色等等，也可以通过左键点击图片，图像下面会提示对应的快捷方式

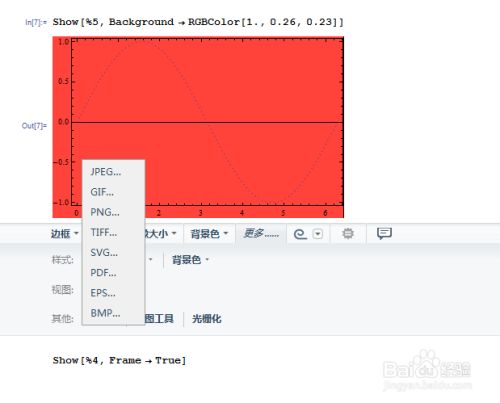
画完图之后，如果想保存图片。mathematica支持大部分图片保存格式，如jpg，eps，pdf等等